На плечах гигантов, на спинах электронов
Об Алане Тьюринге, алгоритмах, машине Тьюринга, тесте Тьюринга, сильном искусственном интеллекте и многом другом
23 июня исполняется 100 лет со дня рождения выдающегося математика, одного из самых ярких основоположников теории алгоритмов, философа искусственного интеллекта Алана Тьюринга . А 7 июня — дата его смерти. Дата публикации записи выбрана таковой по некоторым очевидным соображениям.
Алан Тьюринг человек трагической судьбы, но в этой записи мы остановимся на его научных достижениях. А они чрезвычайно интересны.
1. Машина Тьюринга
читать дальше Представьте себе, что у нас есть бесконечная в обе стороны лента, разделенная на ячейки, в которых записаны символы — буквы из какого-то алфавита. Под алфавитом мы просто понимаем некоторый базисный набор знаков. Помимо символов алфавита, обязательно есть еще особый пустой символ, который заполняет все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.
Представьте себе, что у нас есть бесконечная в обе стороны лента, разделенная на ячейки, в которых записаны символы — буквы из какого-то алфавита. Под алфавитом мы просто понимаем некоторый базисный набор знаков. Помимо символов алфавита, обязательно есть еще особый пустой символ, который заполняет все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.
Вдоль ленты движется каретка, которая называется управляющим устройством. Каретка может читать символы на ленте и записывать туда другие символы алфавита.
Каретка (управляющее устройство (УУ)) может находиться в одном из нескольких состояний, которые описаны заранее. Ее действие для каждой конкретной ячейки определяются символом, записанным в эту ячейку, и текущим состоянием.
Управляющее устройство работает согласно правилам перехода.
За каждый такт оно считывает текущий символ с ленты и в зависимости от своего состояния и значения прочитанного символа выполняет определенное правило перехода: 1) записывает в эту клетку новый символ, 2) переходит в новое состояние и 3) перемещается на одну клетку влево или вправо.
Не обязательно выполнение всех трех пунктов сразу. Содержимое ячейки или состояние УУ вполне могут остаться без изменения.
Описанный "аппарат" и есть Машина Тьюринга.
Машина Тьюринга обязательно должна иметь состояние, переход в которое будет означать конец работы, остановку алгоритма. Таких состояний может быть несколько.
Знаменитый тезис Чёрча-Тьюринга, который говорит о том, что любой мыслимый алгоритм можно реализовать на машине Тьюринга.
Это очень важный результат. Он говорит о том, что какой бы сложный алгоритм мы ни придумали, для абсолютно любого мы можем построить Машину Тьюринга.
(Я описываю всё достаточно неформально. Формальные определения можно посмотреть в литературе по теории алгоритмов).
Алгоритмическая разрешимостьОдним из основных свойств алгоритмов является результативность. Результативность означает, что любой алгоритм рано или поздно должен остановиться (и выдать результат, но это уже побочный продукт факта остановки). Если машина Тьюринга для какой-то задачи остановиться не может, значит, эта проблема алгоритмически неразрешима. И такие проблемы существуют! Но это уже предмет отдельного разговора — с одной стороны это очень интересно, а с другой напрямую касается проблемы создания искусственного интеллекта, к которой Тьюринг тоже причастен!
Проблема остановки, кстати, сама является алгоритмически неразрешимой. Это доказал Тьюринг в 1936 году.
Формально проблему остановки можно описать следующим образом:
Даны описание алгоритма и его начальные входные данные, требуется определить, сможет ли выполнение алгоритма с этими данными завершиться когда-либо. Альтернативой этому является то, что он работает всё время без остановки.
Для решения проблемы остановки не существует общего алгоритма — она неразрешима на машине Тьюринга.
После некоторых дебатов, произошедших несколько лет назад среди модераторов нашего сообщества, мы пришли к выводу, что название l Shift->stop->end l, доставшееся нам по наследству, как раз и описывает завершение работы машины Тьюринга: Сдвиг-Стоп-Завершение. Т.е. сообщество алгоритмически разрешимо
Машина Тьюринга называется детерминированной, если каждой комбинации состояния и ленточного символа соответствует не более одного правила, и недетерминированной в противном случае.
Детерминированность — наряду с результативностью еще одно основное свойство алгоритмов. Говоря просто, это значит, что при выполнении каждого очередного шага, мы точно будем знать, какой шаг мы сделаем следующим. Всё однозначно.
С недетерминированнной машиной Тьюринга дело обстоит иначе.
В ней существуют ситуации, когда устройство управления, встретив в данном состоянии данный символ, может совершить не четко определенную одну вещь, а сразу несколько разных. Поведение машины становится неопределенным. Выбор действия она осуществляет случайным образом.
Иногда рассматривают недетерминированную машину Тьюринга с оракулом. Это означает, что, достигая развилки, машина Тьюринга обращается к оракулу — внешнему устройству, выдающему правильные ответы на некоторый круг вопросов.
При исследовании алгоритмической сложности некоторых задач недетерминированной машине Тьюринга дают подсказку, которая на каждой развилке говорит, какое действие выбрать, чтобы сразу добраться до результата. Эту подсказку, как правило, в виде готового решения, которое нужно только проверить, называют свидетелем.
На практике, однако, поиск свидетелей и построение оракулов — задача не из легких.
2. Расшифровка кода "Энигмы"
читать дальшеМатериал из Википедии
Во время Второй мировой войны Тьюринг работал в Блетчли-парке — британском криптографическом центре, где возглавлял одну из пяти групп, Hut 8, занимавшихся в рамках проекта «Ультра» расшифровкой закодированных немецкой шифровальной машиной «Энигма» сообщений кригсмарине и люфтваффе. Вклад Тьюринга в работы по криптографическому анализу алгоритма, реализованного в «Энигме», основывался на более раннем криптоанализе предыдущих версий шифровальной машины, выполненных в 1938 году польским криптоаналитиком Марианом Реевским.
В начале 1940 года он разработал дешифровальную машину «Бомба», позволявшую читать сообщения люфтваффе. Принцип работы «Бомбы» состоял в переборе возможных вариантов ключа шифра и попыток расшифровки текста, если была известна часть открытого текста или структура расшифровываемого сообщения. Перебор ключей выполнялся за счёт вращения механических барабанов, сопровождавшегося звуком, похожим на тиканье часов, из-за чего «Бомба» и получила свое название. Для каждого возможного значения ключа, заданного положениями роторов (количество ключей равнялось примерно 1019 для сухопутной «Энигмы» и 1022 для шифровальных машин, используемых в подводных лодках), «Бомба» выполняла сверку с известным открытым текстом, выполнявшуюся электрически. Первая в Блетчли «Бомба» Тьюринга была запущена 18 марта 1940 года. Дизайн «Бомб» Тьюринга так же был основан на дизайне одноимённой машины Реевского.
Через полгода удалось взломать и более стойкий шифр Кригсмарине. Позже, к 1943 году, Тьюринг внес ощутимый вклад в создание более совершенной дешифровальной электронно-вычислительной машины «Колосс», использующейся в тех же целях.
3. Теория искусственного интеллекта
3.1. Тест Тьюринга
читать дальшеКартинка из Википедии
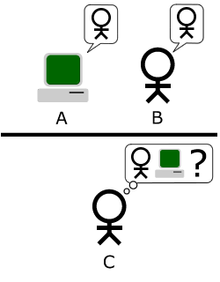 Тест Тьюринга — эмпирический тест, идея которого была предложена Аланом Тьюрингом в статье «Вычислительные машины и разум» (англ. Computing Machinery and Intelligence), опубликованной в 1950 году в философском журнале «Mind». Тест предназначался для ответа на вопрос: можно ли резонно утверждать, что машина думает.
Тест Тьюринга — эмпирический тест, идея которого была предложена Аланом Тьюрингом в статье «Вычислительные машины и разум» (англ. Computing Machinery and Intelligence), опубликованной в 1950 году в философском журнале «Mind». Тест предназначался для ответа на вопрос: можно ли резонно утверждать, что машина думает.
Тест заключается в том, что проницательного человека сажают в пустой комнате за экран монитора.
В соседних комнатах находятся — человек и машина. Точнее "думающий" и "?-думающий" (или "возможно-думающий" ) субъекты. Кто из них где — не известно. Это и надо выяснить опрашивающему.
Общаются они по сети.
Опрашивающий задает всевозможные вопросы, на которые человек отвечает по возможности максимально честно (пытаясь убедить что именно он живое существо). Но то же самое делает компьютер — он хитрит, пытаясь заставить думать тестирующего, что живое существо — это как раз ОН (компьютер).
Если в серии подобных тестов окажется, что опрашивающий не способен "вычислить", кто из двоих — компьютер, то считается, что компьютер (программа) прошел(ла) тест Тьюринга.
Вот как описывает это тест сам Тьюринг в статье "Могут ли машины мыслить":
Эта новая форма может быть описана с помощью игрй, которую мы назовем "игрой в имитацию". В этой игре участвуют три человека: мужчина (А), женщина (Б) и кто-нибудь задающий вопросы (С), которым может быть лицо любого пола. Задающий вопросы отделен от двух других участников игры стенами комнаты, в которой он находится. Цель игры для задающего вопросы состоит в том, чтобы определить, кто из двух других участников игры является мужчиной (А), а кто — женщиной (В). Он знает их под обозначениями Х и У и в конце игры говорит либо: "Х есть А и У есть В", либо: "X есть В и У есть А". Ему разрешается задавать вопросы такого, например, рода:
С: "Попрошу Х сообщить мне длину его (или ее) волос".
Допустим теперь, что в действительности Х есть А. В таком случае А и должен давать ответ. Для А цель игры состоит в том, чтобы побудить С прийти к неверному заключению. Поэтому его ответ может быть, например, таким:
"Мои волосы коротко острижены, а самые длинные пряди имеют около девяти дюймов в длину".
Чтобы задающий вопросы не мог определить по голосу, кто из двух других участников игры мужчина, а кто — женщина, ответы на вопросы следовало бы давать в письменном виде, а еще лучше — на пишущей машинке. Идеальным случаем было бы телеграфное сообщение между двумя комнатами, где находятся участники игры. Если же этого сделать нельзя, то ответы и вопросы должен передавать какой-нибудь посредник. Цель игры для третьего игрока — женщины (В) — состоит в том, чтобы помочь задающему вопросы. Для нее, вероятно, лучшая стратегия — давать правдивые ответы. Она также может делать такие замечания, как "Женщина — я, не слушай- -те его!", но этим она ничего не достигнет, так как мужчина тоже может делать подобные замечания.
Поставим теперь вопрос: "Что произойдет, если в этой игре вместо А будет участвовать машина?" Будет ли в этом случае задающий вопросы ошибаться столь же часто, как и в игре, где участниками являются только люди? Эти вопросы и заменят наш первоначальный вопрос "могут ли машины мыслить?".
А вот статья полностью: А. Тьюринг. Могут ли машины мыслить?
В Википедии тоже много чего интересного можно почерпнуть: Тест Тьюринга. Википедия
3.2. Китайская комната Серла
Естественно, тест Тьюринга казался (и кажется) многим более чем сомнительным свидетельством наличия интеллекта.
3.2.1. Сильный Искусственный интеллект
читать дальшеСуществует такая точка зрения в искусственном интеллекте, которая называется "сильный ИИ". Сторонники сильного ИИ утверждают, что всю мыслительную активность человека можно записать с помощью алгоритма. Понятно, что алгоритм этот ОЧЕНЬ, ЧРЕЗВЫЧАЙНО, сложен, но однако же, если это принципиально возможно, то значит рано или поздно станет осуществимо и технически.
Такой алгоритм, уж вне всяких сомнений пройдет тест Тьюринга.
И, более того, сторонники сильного ИИ уверены, что как только этот алгоритм будет запущен, он начнет сам по себе испытывать чувства, обладать сознанием, быть разумом.
Наиболее остро критиковал эту точку зрения американский философ Джон Серл (он-то и ввел сам термин "сильный искусственный интеллект").
В качестве примера он рассматривает компьютерную программу, разработанную Роджером Шенком. Задача этой программы состояла не просто в ведении осмысленного диалога, но в "понимании ситуаций".
То есть программе давали простые истории, после чего просили сделать небольшое резюме. Вот, к примеру: "Мужчина вошел в ресторан и заказал гамбургер. Когда гамбургер принесли, оказалось, что он сильно подгорел, и рассерженный мужчина выскочил из ресторана, не заплатив по счету и не оставив чаевых". В качестве другого примера следующая история: "Мужчина вошел в ресторан и заказал гамбургер. Когда гамбургер принесли, мужчина остался им очень доволен. И, покидая ресторан, он дал официанту щедрые чаевые перед тем, как заплатить по счету".
Чтобы проверить «понимание» этих историй компьютером, его попросили определить, съел ли мужчина гамбургер в каждом отдельном случае (факт, который не был упомянут в тексте явным образом). На этот простой вопрос компьютер может дать ответ, совершенно не отличающийся от того, что дал бы человек: «нет» в первом случае и «да» — во втором.
То есть в этом узком смысле машина уже прошла тест Тьюринга.
И вот вопрос: действительно ли подобный положительный результат указывает на истинное понимание, демонстрируемое компьютером, или заложенной в него программой?
3.2.2. Китайская комната
читать дальшеКак аргумент в пользу отрицательного ответа Серл и предложил свою концепцию "китайской комнаты".
Серл предложил такой мысленный эксперимент, в котором роль "понимающего компьютера" поручил сам себе.
Итак, он поместил себя в комнату без окон - без дверей, — только с небольшими прорезями.
В эти прорези некие экспериментаторы, которые хотят от него добиться разумного поведения, — просовывают тексты на китайском языке, в котором Серл не понимает ничего. Т.е. ни единого иероглифа.
Никакой другой информации извне он не получает (как и любой компьютер на его месте).
А "тексты", которые ему подают, — не что иное, как истории, которые фигурировали в описании работы Шенка, и вопросы к этим историям, которые он якобы должен понять, чтобы правильно ответить.
Ответы Серла: "да" или "нет" — тоже, естественно, на китайском, — он отдает тоже через эти прорези.
Серл не знает ни слова по-китайски. Но зато у него есть ряд четких инструкций на английском языке, в которых записано, что он должен сделать, получив из прорези некую последовательность символов. Ему важно только правильно сличить.
В итоге, не понимая ни слова по-китайски, он справляется с этой работой не хуже чем любой китаец, способный понять без труда все эти истории и вопросы к ним.
Таким образом, довод Серла состоит в том, что простое выполнение подходящего алгоритма ничего не говорит о понимании.
Он просовывает раз за разом правильные ответы в щели, не понимая ни текстов, ни вопросов к ним.
Вот ссылка на работу Серла "Искусственный интеллект: различные взгляды на проблему"
ИИ: различные взгляды на проблему
Фамилию его (John Rogers Searle) транслитерируют кто во что горазд: Серл, Сёрль, Сирл... Но это не суть важно.
3.2.3. Премия Лёбнера
читать дальшеМатериал из Википедии
Ежегодный конкурс на получение премии Лёбнера является платформой для практического проведения тестов Тьюринга. Первый конкурс прошел в ноябре 1991 года. Приз гарантирован Хью Лёбнером (Hugh Loebner). Кембриджский центр исследований поведения, расположенный в Массачусетсе, США, предоставлял призы до 2003 года включительно. По словам Лёбнера, соревнование было организовано с целью продвижения вперед в области исследований, связанных с искусственным интеллектом, отчасти потому, что «никто не предпринял мер, чтобы это осуществить».
Серебряная (аудио) и золотая (аудио и зрительная) медали никогда ещё не вручались. Тем не менее, ежегодно из всех представленных на конкурс компьютерных систем судьи награждают бронзовой медалью ту, которая, по их мнению, продемонстрирует «наиболее человеческое» поведение в разговоре. Не так давно программа «Искусственное лингвистическое интернет-компьютерное существо» (Artificial Linguistic Internet Computer Entity — A.L.I.C.E.) трижды завоевала бронзовую медаль (в 2000, 2001 и 2004). Способная к обучению программа Jabberwacky побеждала в 2005 и 2006. Её создатели предложили персонализированную версию: возможность пройти имитационный тест, пытаясь более точно сымитировать человека, с которым машина тесно пообщалась перед тестом.
Конкурс проверяет способность разговаривать; победителями становятся обычно чат-боты или «Искусственные разговорные существа» (Artificial Conversational Entities (ACE)s). Правилами первых конкурсов предусматривалось ограничение. Согласно этому ограничению каждая беседа с программой или скрытым человеком могла быть только на одну тему. Начиная с конкурса 1995 года это правило отменено. Продолжительность разговора между судьей и участником была различной в разные годы. В 2003 году, когда конкурс проходил в Университете Суррея, каждый судья мог разговаривать с каждым участником (машиной или человеком) ровно 5 минут. С 2004 по 2007 это время составляло уже более 20 минут. В 2008 максимальное время разговора составляло 5 минут на пару, потому что организатор Кевин Ворвик (Kevin Warwick) и координатор Хьюма Ша (Huma Shah) полагали, что ACE не имели технических возможностей поддерживать более продолжительную беседу. Как ни странно, победитель 2008 года, Elbot, не притворялся человеком, но всё-таки сумел обмануть трех судей. В конкурсе проведенном в 2010 году, было увеличено время до 25 минут при общении между системой и исследователем, по требованию спонсора. А вот в конкурсе проведенном 15 мая 2012 года, состоялось впервые в мире с прямой трансляции беседы, что только поднимает интерес к данному конкурсу.
Появление конкурса на получение премии Лёбнера привело к возобновлению дискуссий о целесообразности теста Тьюринга, о значении его прохождения. В статье «Искусственная тупость» газеты The Economist отмечается, что первая программа-победитель конкурса смогла выиграть отчасти, потому что она «имитировала человеческие опечатки». (Тьюринг предложил, чтобы программы добавляли ошибки в вывод, чтобы быть более хорошими «игроками».) Существовало мнение, что попытки пройти тест Тьюринга просто препятствуют более плодотворным исследованиям.
Во время первых конкурсов была выявлена вторая проблема: участие недостаточно компетентных судей, которые поддавались умело организованным манипуляциям, а не тому, что можно считать интеллектом.
Тем не менее, с 2004 года в качестве собеседников в конкурсе принимают участие философы, компьютерные специалисты и журналисты.
Официальный сайт премии Лёбнера
При создании топика использовались материалы Википедии, книги Роджера Пенроуза "Новый ум короля" и сообщества Поп-математика для взрослых детей
Интересные ссылки из Википедии:
Г. Далидович «Заметки об искусственном интеллекте: маргаритки Тьюринга, Энигма Тьюринга, Яблоко Тьюринга»
23 июня исполняется 100 лет со дня рождения выдающегося математика, одного из самых ярких основоположников теории алгоритмов, философа искусственного интеллекта Алана Тьюринга . А 7 июня — дата его смерти. Дата публикации записи выбрана таковой по некоторым очевидным соображениям.
Алан Мэтисон Тьюринг (англ. Alan Mathison Turing; 23 июня 1912 — 7 июня 1954) — английский математик, логик, криптограф, оказавший существенное влияние на развитие информатики. Кавалер Ордена Британской империи (1945). Предложенная им в 1936 году абстрактная вычислительная «Машина Тьюринга» позволила формализовать понятие алгоритма и до сих пор используется во множестве теоретических и практических исследований. Дата рождения: 23 июня 1912 Место рождения: Лондон, Англия Дата смерти: 7 июня 1954 (41 год) Место смерти: Вилмслоу, Чешир, Англия Страна: Великобритания Научная сфера: математика, логика, криптография Известен как: изобретатель машины Тьюринга, теста Тьюринга (c) Википедия |  |
Алан Тьюринг человек трагической судьбы, но в этой записи мы остановимся на его научных достижениях. А они чрезвычайно интересны.
1. Машина Тьюринга
читать дальше
 Представьте себе, что у нас есть бесконечная в обе стороны лента, разделенная на ячейки, в которых записаны символы — буквы из какого-то алфавита. Под алфавитом мы просто понимаем некоторый базисный набор знаков. Помимо символов алфавита, обязательно есть еще особый пустой символ, который заполняет все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.
Представьте себе, что у нас есть бесконечная в обе стороны лента, разделенная на ячейки, в которых записаны символы — буквы из какого-то алфавита. Под алфавитом мы просто понимаем некоторый базисный набор знаков. Помимо символов алфавита, обязательно есть еще особый пустой символ, который заполняет все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.Вдоль ленты движется каретка, которая называется управляющим устройством. Каретка может читать символы на ленте и записывать туда другие символы алфавита.
Каретка (управляющее устройство (УУ)) может находиться в одном из нескольких состояний, которые описаны заранее. Ее действие для каждой конкретной ячейки определяются символом, записанным в эту ячейку, и текущим состоянием.
Управляющее устройство работает согласно правилам перехода.
За каждый такт оно считывает текущий символ с ленты и в зависимости от своего состояния и значения прочитанного символа выполняет определенное правило перехода: 1) записывает в эту клетку новый символ, 2) переходит в новое состояние и 3) перемещается на одну клетку влево или вправо.
Не обязательно выполнение всех трех пунктов сразу. Содержимое ячейки или состояние УУ вполне могут остаться без изменения.
Описанный "аппарат" и есть Машина Тьюринга.
Машина Тьюринга обязательно должна иметь состояние, переход в которое будет означать конец работы, остановку алгоритма. Таких состояний может быть несколько.
Знаменитый тезис Чёрча-Тьюринга, который говорит о том, что любой мыслимый алгоритм можно реализовать на машине Тьюринга.
Это очень важный результат. Он говорит о том, что какой бы сложный алгоритм мы ни придумали, для абсолютно любого мы можем построить Машину Тьюринга.
(Я описываю всё достаточно неформально. Формальные определения можно посмотреть в литературе по теории алгоритмов).
Алгоритмическая разрешимостьОдним из основных свойств алгоритмов является результативность. Результативность означает, что любой алгоритм рано или поздно должен остановиться (и выдать результат, но это уже побочный продукт факта остановки). Если машина Тьюринга для какой-то задачи остановиться не может, значит, эта проблема алгоритмически неразрешима. И такие проблемы существуют! Но это уже предмет отдельного разговора — с одной стороны это очень интересно, а с другой напрямую касается проблемы создания искусственного интеллекта, к которой Тьюринг тоже причастен!
Проблема остановки, кстати, сама является алгоритмически неразрешимой. Это доказал Тьюринг в 1936 году.
Формально проблему остановки можно описать следующим образом:
Даны описание алгоритма и его начальные входные данные, требуется определить, сможет ли выполнение алгоритма с этими данными завершиться когда-либо. Альтернативой этому является то, что он работает всё время без остановки.
Для решения проблемы остановки не существует общего алгоритма — она неразрешима на машине Тьюринга.
После некоторых дебатов, произошедших несколько лет назад среди модераторов нашего сообщества, мы пришли к выводу, что название l Shift->stop->end l, доставшееся нам по наследству, как раз и описывает завершение работы машины Тьюринга: Сдвиг-Стоп-Завершение. Т.е. сообщество алгоритмически разрешимо

Машина Тьюринга называется детерминированной, если каждой комбинации состояния и ленточного символа соответствует не более одного правила, и недетерминированной в противном случае.
Детерминированность — наряду с результативностью еще одно основное свойство алгоритмов. Говоря просто, это значит, что при выполнении каждого очередного шага, мы точно будем знать, какой шаг мы сделаем следующим. Всё однозначно.
С недетерминированнной машиной Тьюринга дело обстоит иначе.
В ней существуют ситуации, когда устройство управления, встретив в данном состоянии данный символ, может совершить не четко определенную одну вещь, а сразу несколько разных. Поведение машины становится неопределенным. Выбор действия она осуществляет случайным образом.
Иногда рассматривают недетерминированную машину Тьюринга с оракулом. Это означает, что, достигая развилки, машина Тьюринга обращается к оракулу — внешнему устройству, выдающему правильные ответы на некоторый круг вопросов.
При исследовании алгоритмической сложности некоторых задач недетерминированной машине Тьюринга дают подсказку, которая на каждой развилке говорит, какое действие выбрать, чтобы сразу добраться до результата. Эту подсказку, как правило, в виде готового решения, которое нужно только проверить, называют свидетелем.
На практике, однако, поиск свидетелей и построение оракулов — задача не из легких.
2. Расшифровка кода "Энигмы"
читать дальшеМатериал из Википедии
Во время Второй мировой войны Тьюринг работал в Блетчли-парке — британском криптографическом центре, где возглавлял одну из пяти групп, Hut 8, занимавшихся в рамках проекта «Ультра» расшифровкой закодированных немецкой шифровальной машиной «Энигма» сообщений кригсмарине и люфтваффе. Вклад Тьюринга в работы по криптографическому анализу алгоритма, реализованного в «Энигме», основывался на более раннем криптоанализе предыдущих версий шифровальной машины, выполненных в 1938 году польским криптоаналитиком Марианом Реевским.
В начале 1940 года он разработал дешифровальную машину «Бомба», позволявшую читать сообщения люфтваффе. Принцип работы «Бомбы» состоял в переборе возможных вариантов ключа шифра и попыток расшифровки текста, если была известна часть открытого текста или структура расшифровываемого сообщения. Перебор ключей выполнялся за счёт вращения механических барабанов, сопровождавшегося звуком, похожим на тиканье часов, из-за чего «Бомба» и получила свое название. Для каждого возможного значения ключа, заданного положениями роторов (количество ключей равнялось примерно 1019 для сухопутной «Энигмы» и 1022 для шифровальных машин, используемых в подводных лодках), «Бомба» выполняла сверку с известным открытым текстом, выполнявшуюся электрически. Первая в Блетчли «Бомба» Тьюринга была запущена 18 марта 1940 года. Дизайн «Бомб» Тьюринга так же был основан на дизайне одноимённой машины Реевского.
Через полгода удалось взломать и более стойкий шифр Кригсмарине. Позже, к 1943 году, Тьюринг внес ощутимый вклад в создание более совершенной дешифровальной электронно-вычислительной машины «Колосс», использующейся в тех же целях.
3. Теория искусственного интеллекта
3.1. Тест Тьюринга
читать дальшеКартинка из Википедии
 Тест Тьюринга — эмпирический тест, идея которого была предложена Аланом Тьюрингом в статье «Вычислительные машины и разум» (англ. Computing Machinery and Intelligence), опубликованной в 1950 году в философском журнале «Mind». Тест предназначался для ответа на вопрос: можно ли резонно утверждать, что машина думает.
Тест Тьюринга — эмпирический тест, идея которого была предложена Аланом Тьюрингом в статье «Вычислительные машины и разум» (англ. Computing Machinery and Intelligence), опубликованной в 1950 году в философском журнале «Mind». Тест предназначался для ответа на вопрос: можно ли резонно утверждать, что машина думает.Тест заключается в том, что проницательного человека сажают в пустой комнате за экран монитора.
В соседних комнатах находятся — человек и машина. Точнее "думающий" и "?-думающий" (или "возможно-думающий" ) субъекты. Кто из них где — не известно. Это и надо выяснить опрашивающему.
Общаются они по сети.
Опрашивающий задает всевозможные вопросы, на которые человек отвечает по возможности максимально честно (пытаясь убедить что именно он живое существо). Но то же самое делает компьютер — он хитрит, пытаясь заставить думать тестирующего, что живое существо — это как раз ОН (компьютер).
Если в серии подобных тестов окажется, что опрашивающий не способен "вычислить", кто из двоих — компьютер, то считается, что компьютер (программа) прошел(ла) тест Тьюринга.
Вот как описывает это тест сам Тьюринг в статье "Могут ли машины мыслить":
Эта новая форма может быть описана с помощью игрй, которую мы назовем "игрой в имитацию". В этой игре участвуют три человека: мужчина (А), женщина (Б) и кто-нибудь задающий вопросы (С), которым может быть лицо любого пола. Задающий вопросы отделен от двух других участников игры стенами комнаты, в которой он находится. Цель игры для задающего вопросы состоит в том, чтобы определить, кто из двух других участников игры является мужчиной (А), а кто — женщиной (В). Он знает их под обозначениями Х и У и в конце игры говорит либо: "Х есть А и У есть В", либо: "X есть В и У есть А". Ему разрешается задавать вопросы такого, например, рода:
С: "Попрошу Х сообщить мне длину его (или ее) волос".
Допустим теперь, что в действительности Х есть А. В таком случае А и должен давать ответ. Для А цель игры состоит в том, чтобы побудить С прийти к неверному заключению. Поэтому его ответ может быть, например, таким:
"Мои волосы коротко острижены, а самые длинные пряди имеют около девяти дюймов в длину".
Чтобы задающий вопросы не мог определить по голосу, кто из двух других участников игры мужчина, а кто — женщина, ответы на вопросы следовало бы давать в письменном виде, а еще лучше — на пишущей машинке. Идеальным случаем было бы телеграфное сообщение между двумя комнатами, где находятся участники игры. Если же этого сделать нельзя, то ответы и вопросы должен передавать какой-нибудь посредник. Цель игры для третьего игрока — женщины (В) — состоит в том, чтобы помочь задающему вопросы. Для нее, вероятно, лучшая стратегия — давать правдивые ответы. Она также может делать такие замечания, как "Женщина — я, не слушай- -те его!", но этим она ничего не достигнет, так как мужчина тоже может делать подобные замечания.
Поставим теперь вопрос: "Что произойдет, если в этой игре вместо А будет участвовать машина?" Будет ли в этом случае задающий вопросы ошибаться столь же часто, как и в игре, где участниками являются только люди? Эти вопросы и заменят наш первоначальный вопрос "могут ли машины мыслить?".
А вот статья полностью: А. Тьюринг. Могут ли машины мыслить?
В Википедии тоже много чего интересного можно почерпнуть: Тест Тьюринга. Википедия
3.2. Китайская комната Серла
Естественно, тест Тьюринга казался (и кажется) многим более чем сомнительным свидетельством наличия интеллекта.
3.2.1. Сильный Искусственный интеллект
читать дальшеСуществует такая точка зрения в искусственном интеллекте, которая называется "сильный ИИ". Сторонники сильного ИИ утверждают, что всю мыслительную активность человека можно записать с помощью алгоритма. Понятно, что алгоритм этот ОЧЕНЬ, ЧРЕЗВЫЧАЙНО, сложен, но однако же, если это принципиально возможно, то значит рано или поздно станет осуществимо и технически.
Такой алгоритм, уж вне всяких сомнений пройдет тест Тьюринга.
И, более того, сторонники сильного ИИ уверены, что как только этот алгоритм будет запущен, он начнет сам по себе испытывать чувства, обладать сознанием, быть разумом.
Наиболее остро критиковал эту точку зрения американский философ Джон Серл (он-то и ввел сам термин "сильный искусственный интеллект").
В качестве примера он рассматривает компьютерную программу, разработанную Роджером Шенком. Задача этой программы состояла не просто в ведении осмысленного диалога, но в "понимании ситуаций".
То есть программе давали простые истории, после чего просили сделать небольшое резюме. Вот, к примеру: "Мужчина вошел в ресторан и заказал гамбургер. Когда гамбургер принесли, оказалось, что он сильно подгорел, и рассерженный мужчина выскочил из ресторана, не заплатив по счету и не оставив чаевых". В качестве другого примера следующая история: "Мужчина вошел в ресторан и заказал гамбургер. Когда гамбургер принесли, мужчина остался им очень доволен. И, покидая ресторан, он дал официанту щедрые чаевые перед тем, как заплатить по счету".
Чтобы проверить «понимание» этих историй компьютером, его попросили определить, съел ли мужчина гамбургер в каждом отдельном случае (факт, который не был упомянут в тексте явным образом). На этот простой вопрос компьютер может дать ответ, совершенно не отличающийся от того, что дал бы человек: «нет» в первом случае и «да» — во втором.
То есть в этом узком смысле машина уже прошла тест Тьюринга.
И вот вопрос: действительно ли подобный положительный результат указывает на истинное понимание, демонстрируемое компьютером, или заложенной в него программой?
3.2.2. Китайская комната
читать дальшеКак аргумент в пользу отрицательного ответа Серл и предложил свою концепцию "китайской комнаты".
Серл предложил такой мысленный эксперимент, в котором роль "понимающего компьютера" поручил сам себе.
Итак, он поместил себя в комнату без окон - без дверей, — только с небольшими прорезями.
В эти прорези некие экспериментаторы, которые хотят от него добиться разумного поведения, — просовывают тексты на китайском языке, в котором Серл не понимает ничего. Т.е. ни единого иероглифа.
Никакой другой информации извне он не получает (как и любой компьютер на его месте).
А "тексты", которые ему подают, — не что иное, как истории, которые фигурировали в описании работы Шенка, и вопросы к этим историям, которые он якобы должен понять, чтобы правильно ответить.
Ответы Серла: "да" или "нет" — тоже, естественно, на китайском, — он отдает тоже через эти прорези.
Серл не знает ни слова по-китайски. Но зато у него есть ряд четких инструкций на английском языке, в которых записано, что он должен сделать, получив из прорези некую последовательность символов. Ему важно только правильно сличить.
В итоге, не понимая ни слова по-китайски, он справляется с этой работой не хуже чем любой китаец, способный понять без труда все эти истории и вопросы к ним.
Таким образом, довод Серла состоит в том, что простое выполнение подходящего алгоритма ничего не говорит о понимании.
Он просовывает раз за разом правильные ответы в щели, не понимая ни текстов, ни вопросов к ним.
Вот ссылка на работу Серла "Искусственный интеллект: различные взгляды на проблему"
ИИ: различные взгляды на проблему
Фамилию его (John Rogers Searle) транслитерируют кто во что горазд: Серл, Сёрль, Сирл... Но это не суть важно.
3.2.3. Премия Лёбнера
читать дальшеМатериал из Википедии
Ежегодный конкурс на получение премии Лёбнера является платформой для практического проведения тестов Тьюринга. Первый конкурс прошел в ноябре 1991 года. Приз гарантирован Хью Лёбнером (Hugh Loebner). Кембриджский центр исследований поведения, расположенный в Массачусетсе, США, предоставлял призы до 2003 года включительно. По словам Лёбнера, соревнование было организовано с целью продвижения вперед в области исследований, связанных с искусственным интеллектом, отчасти потому, что «никто не предпринял мер, чтобы это осуществить».
Серебряная (аудио) и золотая (аудио и зрительная) медали никогда ещё не вручались. Тем не менее, ежегодно из всех представленных на конкурс компьютерных систем судьи награждают бронзовой медалью ту, которая, по их мнению, продемонстрирует «наиболее человеческое» поведение в разговоре. Не так давно программа «Искусственное лингвистическое интернет-компьютерное существо» (Artificial Linguistic Internet Computer Entity — A.L.I.C.E.) трижды завоевала бронзовую медаль (в 2000, 2001 и 2004). Способная к обучению программа Jabberwacky побеждала в 2005 и 2006. Её создатели предложили персонализированную версию: возможность пройти имитационный тест, пытаясь более точно сымитировать человека, с которым машина тесно пообщалась перед тестом.
Конкурс проверяет способность разговаривать; победителями становятся обычно чат-боты или «Искусственные разговорные существа» (Artificial Conversational Entities (ACE)s). Правилами первых конкурсов предусматривалось ограничение. Согласно этому ограничению каждая беседа с программой или скрытым человеком могла быть только на одну тему. Начиная с конкурса 1995 года это правило отменено. Продолжительность разговора между судьей и участником была различной в разные годы. В 2003 году, когда конкурс проходил в Университете Суррея, каждый судья мог разговаривать с каждым участником (машиной или человеком) ровно 5 минут. С 2004 по 2007 это время составляло уже более 20 минут. В 2008 максимальное время разговора составляло 5 минут на пару, потому что организатор Кевин Ворвик (Kevin Warwick) и координатор Хьюма Ша (Huma Shah) полагали, что ACE не имели технических возможностей поддерживать более продолжительную беседу. Как ни странно, победитель 2008 года, Elbot, не притворялся человеком, но всё-таки сумел обмануть трех судей. В конкурсе проведенном в 2010 году, было увеличено время до 25 минут при общении между системой и исследователем, по требованию спонсора. А вот в конкурсе проведенном 15 мая 2012 года, состоялось впервые в мире с прямой трансляции беседы, что только поднимает интерес к данному конкурсу.
Появление конкурса на получение премии Лёбнера привело к возобновлению дискуссий о целесообразности теста Тьюринга, о значении его прохождения. В статье «Искусственная тупость» газеты The Economist отмечается, что первая программа-победитель конкурса смогла выиграть отчасти, потому что она «имитировала человеческие опечатки». (Тьюринг предложил, чтобы программы добавляли ошибки в вывод, чтобы быть более хорошими «игроками».) Существовало мнение, что попытки пройти тест Тьюринга просто препятствуют более плодотворным исследованиям.
Во время первых конкурсов была выявлена вторая проблема: участие недостаточно компетентных судей, которые поддавались умело организованным манипуляциям, а не тому, что можно считать интеллектом.
Тем не менее, с 2004 года в качестве собеседников в конкурсе принимают участие философы, компьютерные специалисты и журналисты.
Официальный сайт премии Лёбнера
При создании топика использовались материалы Википедии, книги Роджера Пенроуза "Новый ум короля" и сообщества Поп-математика для взрослых детей
Интересные ссылки из Википедии:
Г. Далидович «Заметки об искусственном интеллекте: маргаритки Тьюринга, Энигма Тьюринга, Яблоко Тьюринга»
@темы: История математики, Люди, Ссылки
-
-
15.06.2012 в 12:37название l Shift->stop->end l
Всегда видел в нём какой-то высший смысл)
читать дальше
-
-
15.06.2012 в 12:43-
-
15.06.2012 в 12:53(Про то, что в соавторстве с Хокингом я не говорю. Это совсем другое...)
-
-
15.06.2012 в 13:27Эх, как я вас понимаю!
Дилетант, ты наш культуртрегер!
Спасибо
-
-
15.06.2012 в 13:45Экий изощренный комплимент )))
-
-
15.06.2012 в 13:49-
-
15.06.2012 в 14:24-
-
15.06.2012 в 23:54своих детей из чувства толерантности педофилам и садомитам отдавать чтоли?
-
-
15.06.2012 в 23:57Толерантность - такая непонятная штука.
Но, в любом случае, лучше детей никому не отдавать.
-
-
16.06.2012 в 05:54-
-
16.06.2012 в 08:20-
-
16.06.2012 в 08:30