27.09.2011 в 15:06
Пишет Robot:Диагностическая работа № 1 по математике от 27 сентября 2011 года
Скачать с сайта А.А. Ларина Варианты 1-4, Варианты 5-8 , Варианты 9-12, Варианты 13-16, Критерии без логарифмов , Критерии без производной
C1 (варианты 1,3,5,7,9,11,13,15)
Решите уравнение `6cos^2x-7cosx-5=0`. Укажите корни, принадлежащие отрезку `[-pi;2pi].
C1 (варианты 2,4,6,8,10, 12,14,16)
Решите уравнение `4sin^2x-12sinx+5=0`. Укажите корни, принадлежащие отрезку `[-pi;2pi].
C2 (варианты 1,3,5,7,9,11,13,15)
В правильной шестиугольной призме `ABCDEFA_1B_1C_1D_1E_1F_1`, все рёбра которой равны 4, найдите расстояние от точки `A` до прямой `B_1C_1`
C2 (варианты 2,4,6,8,10,12,14)
В правильной шестиугольной призме `ABCDEFA_1B_1C_1D_1E_1F_1`, все рёбра которой равны 10, найдите расстояние от точки `E` до прямой `B_1C_1`
C3 (варианты 1,3,9,11)
Решите неравенство
`(1/(x^2-7x+12)+(x-4)/(3-x))sqrt(6x-x^2) <=0`
C3 (варианты 2,4,10,12)
Решите систему неравенств
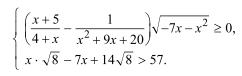
C3 (варианты 5,7,13, 15)
Решите неравенство
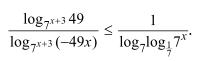
C3 (варианты 6,8,14,16 )
Решите систему неравенств

C4 (варианты 1,3,5,7,9,11,13,15)
Прямая, перпендикулярная гипотенузе прямоугольного треугольника, отсекает от него четырехугольник, в который можно вписать окружность. Найдите радиус окружности, если отрезок этой прямой, заключённый внутри треугольника, равен 14, а отношение катетов
треугольника равно 7/24.
C4 (варианты 2,4,6,8,10,12,14,16)
Прямая, перпендикулярная гипотенузе прямоугольного треугольника, отсекает от него четырехугольник, в который можно вписать окружность. Найдите радиус окружности, если отрезок этой прямой, заключённый внутри треугольника, равен 40, а отношение катетов треугольника равно 15/8.
С5 (варианты 1,3,5,7,9,11,13,15)
Найдите все положительные значения `a`, при каждом из которых система уравнений
`{((|x|-9)^2+(y-5)^2=9),((x+3)^2+y^2=a^2):}
имеет единственное решение.
С5 (варианты 2,4, 6,8,10,12,14,16)
Найдите все значения `a`, при каждом из которых наименьшее значение функции `f(x)=2ax+|x^2-8x+7|` больше 1.
имеет единственное решение.
С6 (варианты 1,3,5,7,9,11,13,15)
Можно ли привести пример пяти различных натуральных чисел, произведение которых равно 1512 и
а) пять;
б) четыре;
в) три
из них образуют геометрическую прогрессию?
С6 (варианты 2,4,6,8,10,12,14,16)
Можно ли привести пример пяти различных натуральных чисел, произведение которых равно 1008 и
а) пять;
б) четыре;
в) три
из них образуют геометрическую прогрессию?
В комментариях ряд решений
URL записи
Пишет к.черный:
27.09.2011 в 21:20

URL комментария

-
-
28.09.2011 в 08:58Решение нескольких задач (вар.9).
С4 Прямая, перпендикулярная гипотенузе прямоугольного треугольника, отсекает от него четырёхугольник, в который можно вписать окружность. Найдите радиус окружности, если отрезок этой прямой, заключённый внутри треугольника, равен 14, а отношение катетов треугольника равно 7/24.
Ответ: 8 или 12,25
Указание. Используя данное соотношение между катетами, легко найти гипотенузу: пусть катеты имеют длины 7x и 24x, тогда гипотенуза треугольника равна 25x. Поскольку окружность, вписанная в получающийся четырехугольник, касается трех сторон исходного треугольника, то она является вписанной в исходный треугольник. Как известно, радиус окружности, вписанной в прямоугольный треугольник, определяется по формуле `r=(a+b-c)/2`, где a,b– катеты, c–гипотенуза. Значит, радиус искомой окружности равен `r=(7x+24x-25x)/2=3x`.
Отсекающая прямая может пересекать либо больший катет, либо меньший катет (см. рис.).
Пусть проведенная прямая переcекает больший катет в точках D и E. Тогда центр вписанной окружности – точка K лежит на диагонали AD четырехугольника ACDE. Действительно, точка K лежит на биссектрисах углов A и CDE, а так как они в сумме составляют 180 градусов, то `/_CAK+/_CDK=90`. Отсюда следует, что четырехугольник ACDE является дельтоидом и AE=AC.Тогда AE=7x, BE=18x=24y (` y`- коэффициент пропорциональности для подобного треугольника). Но тогда DE=7y=14, откуда y=2, x=8/3, r=8.
Пусть проведенная прямая переcекает меньший катет в точках P и Q. Тогда центр вписанной окружности – точка K лежит на диагонали BP четырехугольника BCPQ (доказывается аналогично) и четырехугольник BCPQ является дельтоидом. Значит, BQ=BC. Тогда AQ=x=7y, PQ=24y=14, откуда y=7/12, x=49/12 и r=12.25.
C5 Найдите все положительные значения a, при каждом из которых система уравнений `{((|x|-9)^2+(y-5)^2=9),((x+3)^2+y^2=a^2):}` имеет единственное решение.
Ответ: `a in {sqrt(61)-3;16}`
Указание. Геометрическая интерпретация первого уравнения – две окружности с центрами в точках (±9;5) и радиусом 3. Геометрическая интерпретация второго уравнения – окружность с центром в точке (-3;0) и радиусом a. Единственное решение системы будет в том и только в том случае, когда окружности имеют единственную общую точку, т.е. касаются ( внутренним или внешним образом). Вторая окружность (с центром в точке (-3;0)) имеет общие точки с окружностью с центром (-9;5) при `a in [sqrt(61)-3;sqrt(61)+3]`, а с окружностью с центром (9;5) имеет место при a∈[10;16]. Так как `sqrt(61)+3>10`, то при внутреннем касании второй окружности (с центром в точке (-3;0)) с окружностью с центром (-9;5) (`a=sqrt(61)+3`) она пересекает окружность с центром в точке (9;5) в двух точках, а при внешнем касании с окружностью с центром (9;5) (a=10), пересекает окружность с центром в точке (-9;5) в двух точках. Таким образом, указанная система будет иметь единственное решение при `a in{sqrt(61)-3;16}`
URL комментария
-
-
28.09.2011 в 08:59С1 (варианты 1,3,5,7,9,11,13,15)
Решим тригонометрическое уравнение
Пусть `t=cosx`. Тогда уравнение принимает вид `6t^2-7t-5=0`, откуда `t=-1/2` или `t=5/3`. Возвращаясь к исходной переменной, получаем
`cosx=-1/2` или `cosx=5/3`. Второе уравнение не имеет решений, так как `|cosx|<=1`. Решениями первого уравнения являются две серии: `x=+-2pi/3+2pin, n in Z`
Отбор решений можно провести как помощью тригонометрического круга, либо решая неравенства.
Воспользуемся вторым способом:
1) Отберем корни из серии `x=2pi/3+2pin`, принадлежащие `[-pi;2pi]
Для этого решим неравенство
`-pi<=2pi/3+2pin<=2pi`, откуда
`-1<=2/3+2n<=2`
`-5/3<=2n<=4/3`
`-5/6<=n<=2/3`
Поскольку `n in Z`, то `n=0`и, таким образом, из первой серии указанному промежутку принадлежит только `x=2pi/3`
2)Отберем корни из серии `x=-2pi/3+2pin`, принадлежащие `[-pi;2pi]`
Для этого решим неравенство
`-pi<=-2pi/3+2pin<=2pi`, откуда
`-1<=-2/3+2n<=2`
`-1/3<=2n<=8/3`
`-1/6<=n<=4/3`
Поскольку `n in Z`, то `n=0` или `n=1`и, таким образом, из второй серии указанному промежутку принадлежат `x=-2pi/3`и `x=4pi/3`
Ответ: `x=+-2pi/3+2pin, n in Z`:
корни, принадлежащие `[-pi;2pi]`: `+-2pi/3; 4pi/3`
URL комментария
-
-
28.09.2011 в 09:00C6 Можно ли привести пример пяти различных натуральных чисел, произведение которых равно 1512 и а) пять; б) четыре; в) три из них образуют геометрическую прогрессию?
Ответ: а) нет, б) нет, в) да, например, {1, 3, 7, 8, 9} или {1, 2, 4, 7, 27}
Указание. Имеем: `1512=2^3*3^3*7`.
а) В разложении числа 1512 на простые множители число 7 присутствует только в 1-й степени, а так как число 7 взаимно просто с любыми числами вида `2^k*3^m`, то никакое натуральное число входящее в искомый набор и содержащее 7 в своем разложении, не может быть членом указанной геометрической прогрессии. Поэтому пять членов такая прогрессия содержать не может.
б) Число 7 не может входить в искомую геометрическую прогрессию (объяснено в п.а), поэтому произведение четырех членов геометрической прогрессии содержать только степени чисел 2 и 3 и равно `1512/7=216=2^3*3^3`. Пусть `q=m/n` – знаменатель искомой прогрессии (НОД(m,n)=1). Не нарушая общности можно считать, что искомая прогрессия – монотонно возрастающая. Тогда обозначив первый ее член за b_1, получаем, что произведение ее членов равно `b_1^4∙q^6=b_1^4*m^6/n^6` . В силу взаимной простоты чисел m и n, получаем, что `n^6` является делителем числа `b_1^4`. Однако, ни одного простого множителя в четвертой степени число 216 не содержит, поэтому число `b_1` не может быть натуральным числом. Значит, четырех членов геометрической прогрессии здесь быть не может.
в) Набор из пяти чисел с заданным произведением, три из которых являются членами некоторой геометрической прогрессии, строится легко, например, {1, 3, 7, 8, 9} или {1, 2, 4, 7, 27}.
URL комментария
-
-
28.09.2011 в 09:01C5 (вар.10). Найдите все значения a, при каждом из которых наименьшее значение функции `f(x)=2ax+|x^2-8x+7|` больше 1.
Ответ: `a in (0,5;4+sqrt(6))`
Указание. Функция f(x) определена на R, поэтому условие задачи равносильно такому:
Найдите все значения a, при каждом из которых для любых `x in R` выполняется неравенство `2ax+|x^2-8x+7|>1`. Перепишем неравенство в виде `2ax>1-|x^2-8x+7|` и воспользуемся графической иллюстрацией для решения (см. рис.).
Так, как функция `g(x)=1-|x^2-8x+7|` принимает наибольшие значения в точках `x in{1;7}`, то неравенство будет выполняться, если одновременно выполняются условия: `{(2a>g(1)),(2a*7>g(7)):}`, откуда a>0.5.
Найдем точку касания. Имеем: `{(f(x)=g(x)),(f^' (x)=g^' (x)):}` или `{(2ax=-x^2+8x-6),(2a=-2x+8):}`. Исключая из указанной системы точку x получаем для параметра a уравнение `a^2-8a+10=0`, откуда `a=4∓sqrt(6)`. В случае `a=4-sqrt(6)` точка касания `x_k=sqrt(6)` лежит правее точки x=1. Значит , `a in (0,5;4+sqrt(6))` ( условие задачи выполняется если график функции g(x) на участке (-∞;1) лежит ниже касательной к графику).
URL комментария
-
-
28.09.2011 в 09:02C2(варианты 1,3,5,7,9,11,13,15)
В правильной шестиугольной призме `ABCDEFA_1B_1C_1D_1E_1F_1`, все рёбра которой равны 4, найдите расстояние от точки `A` до прямой `B_1C_1`
Решение.
Прямая `AD` параллельна прямой `BC`, которая, в свою очередь, параллельна `C_1B_1`, поэтому `AD || B_1C_1`, значит, все точки этой прямой находятся на одинаковом расстоянии от прямой `B_1C_1`, следовательно, расстояние от A до `B_1C_1` равно расстоянию от О до этой прямой. Проведем `OP_|_BC`(легко доказать, что Р - середина `BC`) и `PK||B B_1`. Соединим О и K. Так как `B B_1` перпендикуляр к плоскости основания, то и `KP` тоже будет перпендикуляром к ней, а потому `OP` -проекция наклонной `OK`, а тогда по теореме о трех перпендикулярах `OK_|_BC`, и в силу параллельности `BC` и `B_1C_1` `OK_|_B_1C_1`
Найдем ОК из прямоугольного треугольника `KPO`: `PK=4`, `OP=2sqrt(3)` (из прямоугольного треугольника `OPB`), откуда `OK=2*sqrt(7)`
Ответ: `2*sqrt(7)`
URL комментария
-
-
08.11.2011 в 18:08Ответ: `2*sqrt(7)`
Как ты это нашел? поясни плз
-
-
08.11.2011 в 19:29Там используется теорема Пифагора.
-
-
08.11.2011 в 20:50-
-
08.11.2011 в 20:53-
-
08.11.2011 в 21:04прроошу подробнее очень надо
-
-
08.11.2011 в 21:18-
-
08.11.2011 в 21:33-
-
08.11.2011 в 21:41Вообще незанкомые слова можно узнать, набрав их в поисковой строке браузера. Google, Яndex, и т.д.
-
-
08.11.2011 в 21:46-
-
08.11.2011 в 21:49-
-
08.11.2011 в 21:50http://ru.wikipedia.org
www.bymath.net/studyguide/geo/sec/geo11.htm
-
-
08.11.2011 в 21:51-
-
08.11.2011 в 21:55-
-
08.11.2011 в 21:56ИЗУЧИТЕ все, что касается правильного шестиугольника
Бессмысленно приступать к части С, не зная элементарных вещей
Пока комментарии закрываю
-
-
20.11.2011 в 18:03-
-
17.05.2012 в 15:08-
-
17.05.2012 в 17:18Во-вторых, если у Вас есть вопросы по конкретным задачам, то эту задачу надо задать с главной страницы. На этот топик сейчас подписано всего 2 человека и Ваш вопрос будет неизвестен в сообществе.
-
-
26.04.2014 в 11:11